We find that a highly simplified transformer neural network is able to compute Conway’s Game of Life perfectly, just from being trained on examples of the game.
The simple nature of this model allows us to look at its structure and observe that it really is computing the Game of Life — it is not a statistical model that predicts the most likely next state based on all the examples it has been trained on.
We observe that it learns to use its attention mechanism to compute 3x3 convolutions — 3x3 convolutions
are a common way to implement the Game of Life, since it can be used to count the neighbours of a cell, which is used to decide whether the cell lives or dies.
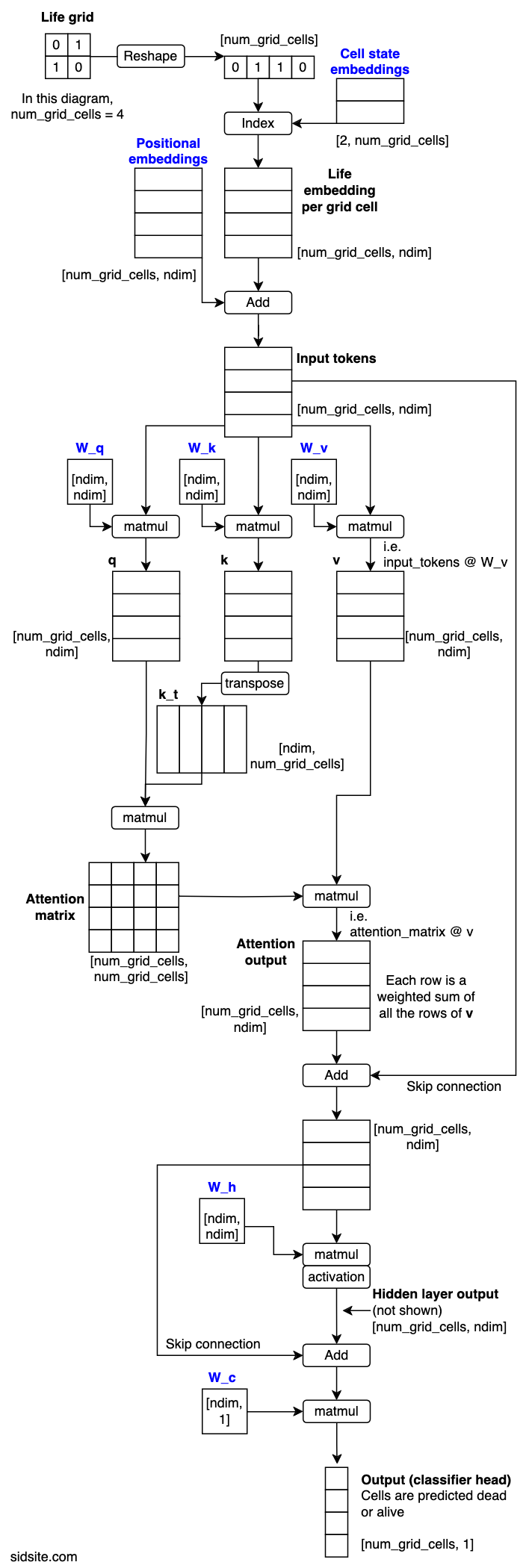
We refer to the model as SingleAttentionNet, because it consists of a single attention block, with single-head attention. The model represents a Life grid as a set of tokens, with one token per grid cell.
The following figure shows a Life game, computed by a SingleAttentionNet model:

The following figure shows examples of the SingleAttentionNet model’s attention matrix, over the course of training:

This shows the model learning to compute a 3 by 3 average pool via its attention mechanism, (with the middle cell excluded from the average).
Details
The full code is made available, here.
The problem is modeled as:
model(life_grid) = next_life_grid
Where gradient descent is used to minimize the loss:
loss = cross_entropy(true_next_life_grid, predicted_next_life_grid)
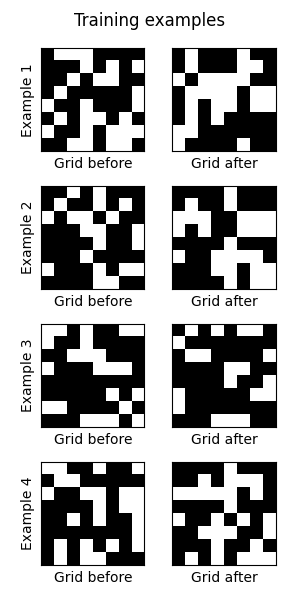
Life grids are generated randomly, to provide a limitless source of training pairs,
(life_grid, next_life_grid). Some examples:
Model diagram
The model in the diagram processes 2-by-2 Life grids, which means 4 tokens in total per grid. Blue text indicates parameters that are learned via gradient descent. The arrays are labelled with their shape, (with the batch dimension omitted).
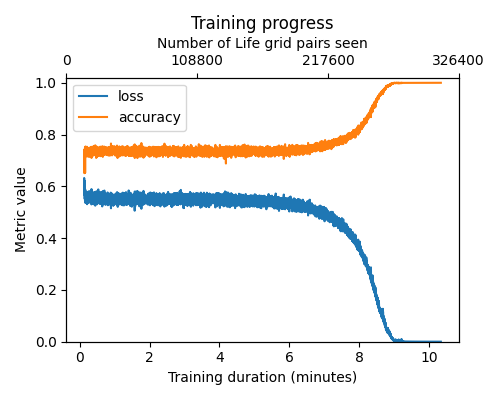
Training
On a GPU, training the model takes anywhere from a couple of minutes, to 10 minutes, or fails to converge, depending on the seed and other training hyperparameters. The largest grid size we successfully trained was 16x16.
Notes
We tried replacing the attention layer of the model with a manually computed Neighbour Attention matrix, and found the model learned its task far quicker, and generalised to arbitrary grid sizes. We found that the same was true for replacing the layer with a 3-by-3 average pool.
We detected that the model had converged by looking for 1024 training batches with perfect predictions,
and that it could perfectly run 100 Life games for 100 steps.
We found that it was enough to train the model on the first and second iterations of the random Life games, but it wasn’t enough to just train on the first iterations.
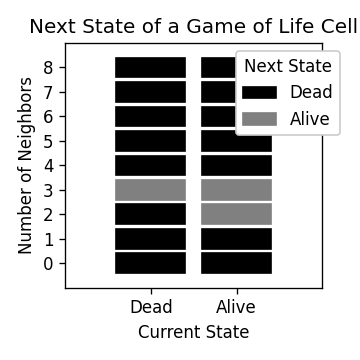
The rules of Life
Life takes place on a 2D grid with cells that are either dead or alive, (represented by 0 or 1). A cell has 8 neighbours, which are the cells immediately next to it on the grid.
To progress to the next Life step, the following rules are used:
- If a cell has 3 neighbours, it will be alive in the next step, regardless of it’s current state, (alive or dead).
- If a cell is alive and has 2 neighbours, it will stay alive in the next step.
- Otherwise, a cell will be dead in the next step.
These rules are shown in the following plot.
References:
Citation:
@misc{radcliffe_life_transformer_2024,
title={Training a Simple Transformer Neural Net on Conway's Game of Life},
url={https://sidsite.com/posts/life-transformer/},
howpublished={Main page: \url{https://sidsite.com/posts/life-transformer/}, GitHub repository: \url{https://github.com/sradc/life-transformer}},
author={Radclffe, Sidney},
year={2024},
month={July}
}
